Draw a Circle of Radius R Centered at the Origin

Circle Cartoon Algorithms-

In estimator graphics, popular algorithms used to generate circle are-

1. Mid Point Circle Drawing Algorithm
2. Bresenham'southward Circumvolve Drawing Algorithm

In this commodity, we will talk over about Mid Point Circle Drawing Algorithm.

Mid Point Circumvolve Drawing Algorithm-

Given the centre point and radius of circle,

Mid Indicate Circle Cartoon Algorithm attempts to generate the points of one octant.

The points for other octacts are generated using the eight symmetry property.

Process-

Given-

• Center indicate of Circle = (X₀, Y₀)
• Radius of Circle = R

The points generation using Mid Point Circle Drawing Algorithm involves the following steps-

Pace-01:

Assign the starting point coordinates (X₀, Y₀) as-

• X₀ = 0
• Y₀ = R

Pace-02:

Calculate the value of initial decision parameter P₀ every bit-

P₀ = ane – R

Step-03:

Suppose the current point is (X_k, Y₁₀₀₀) and the next betoken is (10_grand+one, Y_k+1).

Detect the side by side point of the first octant depending on the value of determination parameter P_k.

Follow the below 2 cases-

Step-04:

If the given middle betoken (10₀, Y₀) is not (0, 0), then do the post-obit and plot the indicate-

• X_plot = 10_c + X₀
• Y_plot = Y_c + Y₀

Hither, (X_c, Y_c) denotes the current value of X and Y coordinates.

Step-05:

Keep repeating Step-03 and Footstep-04 until X_plot >= Y_plot.

Pace-06:

Step-05 generates all the points for one octant.

To detect the points for other seven octants, follow the eight symmetry property of circle.

This is depicted past the following figure-

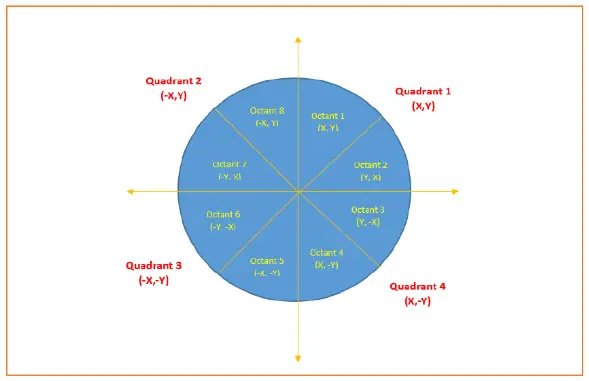
Also Read- Line Cartoon Algorithms

Practise Problems BASED ON MID POINT Circumvolve DRAWING ALGORITHM-

Trouble-01:

Given the center point coordinates (0, 0) and radius as x, generate all the points to form a circumvolve.

Solution-

Given-

• Eye Coordinates of Circle (X₀, Y₀) = (0, 0)
• Radius of Circle = 10

Step-01:

Assign the starting point coordinates (X₀, Y₀) equally-

• X₀ = 0
• Y₀ = R = ten

Pace-02:

Calculate the value of initial conclusion parameter P₀ as-

P₀ = i – R

P₀ = 1 – ten

P₀ = -9

Step-03:

As P_initial < 0, so example-01 is satisfied.

Thus,

• X_chiliad+i = 10_k + one = 0 + 1 = 1
• Y_chiliad+1 = Y_thousand = 10
• P_{one thousand+1} = P_k + two ten X_{one thousand+1} + i = -ix + (2 x 1) + 1 = -6

Step-04:

This footstep is not applicable here as the given eye point coordinates is (0, 0).

Stride-05:

Stride-03 is executed similarly until X₁₀₀₀₊₁ >= Y_k+i equally follows-

Pthou	Pyard+1	(Xk+1, Ythousand+i)
		(0, 10)
-9	-6	(ane, 10)
-6	-1	(2, x)
-1	half dozen	(3, 10)
half-dozen	-3	(four, 9)
-three	viii	(5, nine)
eight	5	(vi, viii)
Algorithm Terminates These are all points for Octant-1.

Algorithm calculates all the points of octant-1 and terminates.

Now, the points of octant-two are obtained using the mirror result by swapping X and Y coordinates.

Octant-one Points	Octant-2 Points
(0, x)	(8, six)
(1, 10)	(nine, v)
(2, x)	(9, 4)
(3, 10)	(x, 3)
(4, 9)	(10, 2)
(5, nine)	(x, ane)
(half dozen, 8)	(10, 0)
These are all points for Quadrant-1.

At present, the points for rest of the part are generated by following the signs of other quadrants.

The other points can likewise be generated by calculating each octant separately.

Here, all the points have been generated with respect to quadrant-i-

Quadrant-i (X,Y)	Quadrant-ii (-Ten,Y)	Quadrant-3 (-X,-Y)	Quadrant-4 (10,-Y)
(0, 10)	(0, 10)	(0, -x)	(0, -10)
(1, 10)	(-ane, 10)	(-1, -10)	(1, -x)
(2, 10)	(-2, 10)	(-2, -10)	(two, -10)
(3, 10)	(-three, 10)	(-3, -10)	(3, -10)
(4, 9)	(-4, 9)	(-4, -9)	(four, -9)
(v, 9)	(-5, 9)	(-five, -9)	(five, -9)
(6, 8)	(-six, 8)	(-6, -viii)	(half-dozen, -8)
(8, 6)	(-8, 6)	(-eight, -vi)	(8, -six)
(nine, 5)	(-nine, 5)	(-9, -v)	(9, -v)
(9, four)	(-9, 4)	(-9, -four)	(9, -four)
(ten, 3)	(-x, 3)	(-10, -three)	(10, -3)
(10, 2)	(-10, 2)	(-10, -two)	(10, -two)
(ten, i)	(-10, 1)	(-10, -ane)	(ten, -1)
(10, 0)	(-x, 0)	(-10, 0)	(10, 0)
These are all points of the Circle.

Problem-02:

Given the centre point coordinates (iv, -four) and radius equally 10, generate all the points to form a circle.

Solution-

Given-

• Centre Coordinates of Circle (X₀, Y₀) = (iv, -4)
• Radius of Circle = 10

As stated in the algorithm,

• We showtime calculate the points bold the center coordinates is (0, 0).
• At the stop, we interpret the circumvolve.

Footstep-01, Stride-02 and Step-03 are already completed in Problem-01.

Now, we notice the values of X_plot and Y_plot using the formula given in Pace-04 of the main algorithm.

The post-obit tabular array shows the generation of points for Quadrant-i-

• X_plot = X_c + X₀ = iv + Ten₀
• Y_plot = Y_c + Y₀ = 4 + Y₀

(Xk+one, Yk+1)	(Xplot, Yplot)
(0, 10)	(4, 14)
(1, 10)	(5, fourteen)
(2, 10)	(6, 14)
(3, 10)	(7, 14)
(4, ix)	(8, 13)
(v, 9)	(9, 13)
(6, 8)	(10, 12)
(8, 6)	(12, 10)
(nine, 5)	(13, 9)
(9, iv)	(xiii, 8)
(10, 3)	(14, 7)
(10, 2)	(14, 6)
(10, i)	(fourteen, 5)
(ten, 0)	(14, 4)
These are all points for Quadrant-i.

The following tabular array shows the points for all the quadrants-

Quadrant-1 (10,Y)	Quadrant-2 (-X,Y)	Quadrant-3 (-Ten,-Y)	Quadrant-iv (X,-Y)
(iv, 14)	(iv, 14)	(four, -vi)	(4, -half-dozen)
(5, xiv)	(iii, 14)	(3, -6)	(5, -half-dozen)
(six, 14)	(ii, 14)	(2, -6)	(half dozen, -6)
(vii, 14)	(1, 14)	(1, -6)	(7, -6)
(8, 13)	(0, 13)	(0, -5)	(eight, -5)
(9, thirteen)	(-1, 13)	(-ane, -5)	(nine, -5)
(ten, 12)	(-2, 12)	(-2, -4)	(ten, -4)
(12, 10)	(-iv, 10)	(-4, -ii)	(12, -2)
(13, 9)	(-5, 9)	(-5, -1)	(13, -1)
(13, 8)	(-5, eight)	(-5, 0)	(13, 0)
(14, 7)	(-6, 7)	(-6, 1)	(xiv, i)
(14, 6)	(-half dozen, six)	(-6, 2)	(14, ii)
(14, 5)	(-half dozen, 5)	(-vi, 3)	(14, 3)
(fourteen, 4)	(-six, 4)	(-6, four)	(14, 4)
These are all points of the Circle.

Advantages of Mid Point Circle Cartoon Algorithm-

The advantages of Mid Signal Circumvolve Drawing Algorithm are-

• Information technology is a powerful and efficient algorithm.
• The entire algorithm is based on the simple equation of circle Ten^two + Y² = R².
• It is piece of cake to implement from the programmer'southward perspective.
• This algorithm is used to generate curves on raster displays.

Disadvantages of Mid Indicate Circle Drawing Algorithm-

The disadvantages of Mid Point Circle Drawing Algorithm are-

• Accuracy of the generating points is an effect in this algorithm.
• The circle generated by this algorithm is non smooth.
• This algorithm is time consuming.

Important Points

• Circle drawing algorithms have the advantage of 8 symmetry holding of circumvolve.
• Every circle has 8 octants and the circle cartoon algorithm generates all the points for ane octant.
• The points for other 7 octants are generated by changing the sign towards X and Y coordinates.
• To take the advantage of 8 symmetry belongings, the circle must exist formed assuming that the centre betoken coordinates is (0, 0).
• If the centre coordinates are other than (0, 0), and then we add together the Ten and Y coordinate values with each bespeak of circle with the coordinate values generated by assuming (0, 0) every bit centre point.

To proceeds meliorate understanding about Mid Point Circle Drawing Algorithm,

Watch this Video Lecture

Next Commodity- Bresenham Circle Drawing Algorithm

Get more notes and other study fabric of Calculator Graphics.

Lookout man video lectures by visiting our YouTube channel LearnVidFun.

Summary

Article Proper noun

Mid Point Circle Cartoon Algorithm

Description

Circle Drawing Algorithms- Midpoint Circle Cartoon Algorithm is a famous circle drawing algorithm. Midpoint Circle Cartoon Algorithm takes the middle indicate & radius of circumvolve and generates the points for one octant.

Author

Akshay Singhal

Publisher Name

Gate Vidyalay

Publisher Logo

maloneyhisibut.blogspot.com

Source: https://www.gatevidyalay.com/mid-point-circle-drawing-algorithm/