Function That is Continuous Only at Irrational Points
Dirichlet function and its modifications
We start with the definition of the Dirichlet function.
Definition.
The Dirichlet function is defined by
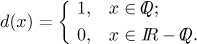
Note that both rational numbers (where

Since there are rational and irrational points everywhere, these two "lines" have in fact holes in them; these holes are everywhere, there is never even a tiny piece of uninterrputed line. Indeed, concerning the upper "line", every time we take two rational numbers, there will always be some irrational number between them making a hole in the upper "line". Similarly, between every two irrational numbers, however close to each other, there is always some rational, making a hole in the lower "line".
So there are holes everywhere, but these holes are always of single-point size, they never form a bigger hole, for the same reasons as above. For instance, when we take two holes in the upper "line", they correspond to two irrational numbers, and since there is surely some rational number between them, it will make a dot in the upper "line" separating the two holes.
What are the properties of this function? First note that there is not a single point where we would have any one-sided limit. Indeed, pick some number a. In arbitrary neighborhood of a (also one-sided) we find both rational and irrational numbers, so on this neighborhood d oscillates between 0 and 1. Because this oscillation cannot be decreased by making the neighborhood smaller, there is no limit at a, not even one-sided.
Since we do not have limits, we also cannot have continuity (even one-sided), that is, the Dirichlet function is not continuous at a single point. Consequently we do not have derivatives, not even one-sided.
There is also no point where this function would be monotone. Indeed, pick some a, say rational. Then
Another interesting property is that d is
On the other hand, this function is not
In this note we actually prove that this function is not Riemann integrable on any interval.
Modification 1
Define
![]()
This function looks like this:
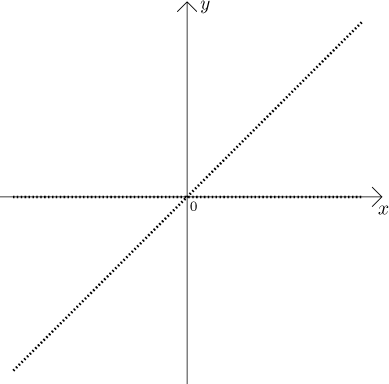
This time we did not draw continuous lines but made them dotted to suggest the scattered nature of the graph, but this one is as misguiding as the previous graph with full lines, because now we have to remember that there are no holes as indicated, what we see as holes is full of dots. Now at rational numbers the dots lie on the line
Modification 2
Define
![]()
This function looks like this:
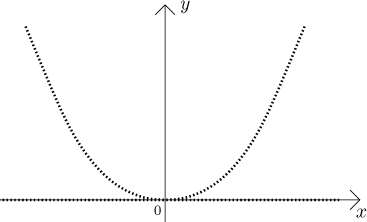
Here the dots corresponding to rational numbers follow the parabola, while the irrational dots are again at zero level. Away from zero, this function is still as bad as the Dirichlet function, but now we even have a derivative at the origin, namely
This again shows that the existence of derivative at a point does not guaranteee that the function will be nice even on a tiny neighborhood of that point.
Modification 3
Define
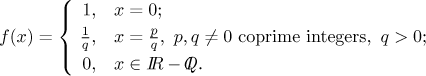
This function is somewhat different. At irrational numbers it is zero, but at other points it is a different story. To imagine it better, we will look at values at various points. To make our task easier, we first show that this function is
If x is an irrational number, then
Consequently, this function is
Having the periodicity out of the way, we now know that it is enough to know how the graph looks like on [0,1]. We know that at irrational points we get zero, what about other points? We have
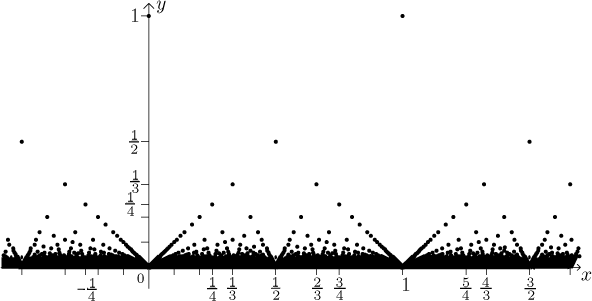
There are more and more points as we look lower, closer to the x-axis, so the graph is quickly becoming quite a mess.
What are the properties of this function? Surprising as it sounds, at every point a we have a limit, namely zero. Since this is the core property of this function and it sounds a bit unbelievable, we will include a proof of this fact at the end as an Appendix.
It follows that this function is continuous exactly at points where it has value 0, therefore f is continuous at all irrational points and discontinuous at rational points. Since we have limits there, we see that these discontinuities are all of the removable kind. This is so weird that we feel it to be the fitting conclusion to our freak zoo.
Appendix
Here we prove that for every a, the function f has limit 0 at a. Indeed, assume that somebody gave us a tolerance
First, find some natural number r so that
Is this δ the right one? Pick any x from this neighborhood. If x is irrational, then
The proof is complete.
Back to Theory - Elementary functions
Source: https://math.fel.cvut.cz/mt/txtb/4/txe3ba4s.htm
Publicar un comentario for "Function That is Continuous Only at Irrational Points"